Dynamical systems approaches for deep learning

Summary

Under the supervision of Professor Randy Paffenroth, my senior thesis explores iterative neural networks (INNs), which reimagine neural network designs as iterated functions. We investigate the effects of sparse and low-rank matrix approximations on model performance, particularly focusing on sparsity and weight distribution using the MNIST Random Anomaly Task.

Our results highlight the delicate balance between parallelization advantages and the need for equitable weight distribution. The comparison of sparse, low rank, and dense matrices reveals low-rank matrices’ role in boosting computational speed without drastically affecting model accuracy. Overall, this research advances our understanding of INNs, underlining the significance of matrix representation methods in providing more interpretable finetuning strategies, as well as improved performance.

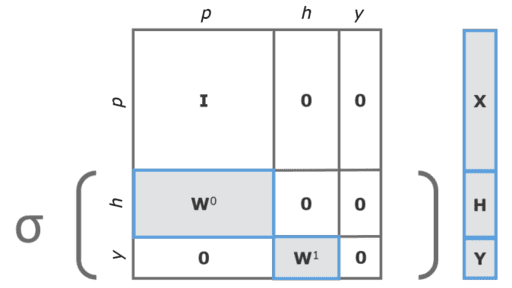
Figure. A two-layer multilayer perceptron (MLP) represented as a 3x3 iterative neural network.